ujian telah selesai dilaksanakan selama 28 november-08 desember, tapi para generasi muda skrng masih asyik belajar😊 (semangat kakak" buat tugas remedinya...😁😂).
smg cepat kelar ya kk tugas remedi matematikanya....!
15 desember 2016
#kekenandyuta
#smamuhammadiyah1yogyakarta
smg cepat kelar ya kk tugas remedi matematikanya....!
15 desember 2016
#kekenandyuta
#smamuhammadiyah1yogyakarta
A. UNSUR - UNSUR ALJABAR
1. Variabel, Konstanta, dan Faktor
Perhatikan bentuk aljabar 5x + 3y + 8x – 6y + 9. Pada bentuk aljabar tersebut, huruf x dan y disebut variabel. Variabel adalah lambang pengganti suatu bilangan yang belum diketahui nilainya dengan jelas. Variabel disebut juga peubah. Variabel biasanya dilambangkan dengan huruf kecil a, b, c, ..., z.
Adapun bilangan 9 pada bentuk aljabar di atas disebut konstanta. Konstanta adalah suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel. Jika suatu bilangan a dapat diubah menjadi a = p X q dengan a, p, q bilangan bulat, maka p dan q disebut faktor-faktor dari a.
Pada bentuk aljabar di atas, 5x dapat diuraikan sebagai 5x = 5 X x atau 5x = 1 X 5x. Jadi, faktor-faktor dari 5x adalah 1, 5, x, dan 5x. Adapun yang dimaksud koefisien adalah faktor konstanta dari suatu suku pada bentuk aljabar. Perhatikan koefisien masing-masing suku pada bentuk aljabar 5x + 3y + 8x – 6y + 9. Koefisien pada suku 5x adalah 5, pada suku 3y adalah 3, pada suku 8x adalah 8, dan pada suku –6y adalah –6.
2. Suku Sejenis dan Suku Tak Sejenis
a) Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.
a) Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.
Suku-suku sejenis adalah suku yang memiliki variabel dan pangkat dari masing-masing variabel yang sama. Contoh: 5x dan –2x, 3a2 dan a2, y dan 4y, ...
Suku tak sejenis adalah suku yang memiliki variabel dan pangkat dari masing-masing variabel yang tidak sama. Contoh: 2x dan –3x2, –y dan –x3, 5x dan –2y, ...
b) Suku satu adalah bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih. Contoh: 3x, 2a2, –4xy, ...
c) Suku dua adalah bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih. Contoh: 2x + 3, a2 – 4, 3x2 – 4x, ...
d) Suku tiga adalah bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih. Contoh: 2x2 – x + 1, 3x + y – xy, ...
Bentuk aljabar yang mempunyai lebih dari dua suku disebut suku banyak.
B. OPERASI HITUNG PADA ALJABAR
1. Penjumlahan dan Pengurangan Bentuk Aljabar
Pada bentuk aljabar, operasi penjumlahan dan pengurangan hanya dapat dilakukan pada suku-suku yang sejenis. Jumlahkan atau kurangkan koefisien pada suku-suku yang sejenis.
2. Perkalian
Perlu kalian ingat kembali bahwa pada perkalian bilangan bulat berlaku sifat distributif perkalian terhadap penjumlahan, yaitu a X (b + c) = (a X b) + (a X c) dan sifat distributif perkalian terhadap pengurangan, yaitu a X (b – c) = (a X b) – (a X c), untuk setiap bilangan bulat a, b, dan c. Sifat ini juga berlaku pada perkalian bentuk aljabar.
3. Perpangkatan
 Coba kalian ingat kembali operasi perpangkatan pada bilangan bulat. Operasi perpangkatan diartikan sebagai perkalian berulang dengan bilangan yang sama. Hal ini juga berlaku pada perpangkatan bentuk aljabar. Pada perpangkatan bentuk aljabar suku dua, koefisien tiap suku ditentukan menurut segitiga Pascal. Misalkan kita akan menentukan pola koefisien pada penjabaran bentuk aljabar suku dua (a + b)n, dengan n bilangan asli.
Coba kalian ingat kembali operasi perpangkatan pada bilangan bulat. Operasi perpangkatan diartikan sebagai perkalian berulang dengan bilangan yang sama. Hal ini juga berlaku pada perpangkatan bentuk aljabar. Pada perpangkatan bentuk aljabar suku dua, koefisien tiap suku ditentukan menurut segitiga Pascal. Misalkan kita akan menentukan pola koefisien pada penjabaran bentuk aljabar suku dua (a + b)n, dengan n bilangan asli.
Perhatikan uraian berikut:
Pada segitiga Pascal tersebut, bilangan yang berada di bawahnya diperoleh dari penjumlahan bilangan yang berdekatan yang berada di atasnya.
4. Pembagian
Hasil bagi dua bentuk aljabar dapat kalian peroleh dengan menentukan terlebih dahulu faktor sekutu masing-masing bentuk aljabar tersebut, kemudian melakukan pembagian pada pembilang dan penyebutnya.
5. Substitusi pada Bentuk Aljabar
Nilai suatu bentuk aljabar dapat ditentukan dengan cara menyubstitusikan sebarang bilangan pada variabel-variabel bentuk aljabar tersebut.
6. Menentukan KPK dan FPB Bentuk Aljabar
Coba kalian ingat kembali cara menentukan KPK dan FPB dari dua atau lebih bilangan bulat. Hal itu juga berlaku pada bentuk aljabar. Untuk menentukan KPK dan FPB dari bentuk aljabar dapat dilakukan dengan menyatakan bentuk-bentuk aljabar tersebut menjadi perkalian faktor-faktor primanya. Perhatikan contoh berikut:
C. PECAHAN BENTUK ALJABAR
1. Menyederhanakan Pecahan Bentuk Aljabar
Suatu pecahan bentuk aljabar dikatakan paling sederhana apabila pembilang dan penyebutnya tidak mempunyai faktor persekutuan kecuali 1, dan penyebutnya tidak sama dengan nol. Untuk menyederhanakan pecahan bentuk aljabar dapat dilakukan dengan cara membagi pembilang dan penyebut pecahan tersebut dengan FPB dari keduanya.
2. Operasi Hitung Pecahan Aljabar dengan Penyebut Suku Tunggal
a. Penjumlahan dan pengurangan
Pada bab sebelumnya, kalian telah mengetahui bahwa hasil operasi penjumlahan dan pengurangan pada pecahan diperoleh dengan cara menyamakan penyebutnya, kemudian menjumlahkan atau mengurangkan pembilangnya. Kalian pasti juga masih ingat bahwa untuk menyamakan penyebut kedua pecahan, tentukan KPK dari penyebut-penyebutnya. Dengan cara yang sama, hal itu juga berlaku pada operasi penjumlahan dan pengurangan bentuk pecahan aljabar. Perhatikan contoh berikut:
b. Perkalian dan pembagian
Perkalian pecahan aljabar tidak jauh berbeda dengan perkalian bilangan pecahan. Perhatikan contoh berikut:
Perkalian pecahan aljabar tidak jauh berbeda dengan perkalian bilangan pecahan. Perhatikan contoh berikut:
c. Perpangkatan pecahan bentuk aljabar
 Operasi perpangkatan merupakan perkalian berulang dengan bilangan yang sama. Hal ini juga berlaku pada perpangkatan pecahan bentuk aljabar. Perhatikan contoh berikut:
Operasi perpangkatan merupakan perkalian berulang dengan bilangan yang sama. Hal ini juga berlaku pada perpangkatan pecahan bentuk aljabar. Perhatikan contoh berikut:
kali ini kita akan membahas tentang operasi hitung pada pecahan. Apa sih pecahan?.... Pecahan adlah istilah dalam matematika yang terdiri dari pembilang dan penyebut.
A.operasi pada penjumlahan

dalam operasi ini kita harus menyamakan penyebutnya terlebih dahulu.dengan cara mencari kpk dari masing-masing penyebut tersebut,setelah itu baru kita bisa mengoperasikannya.
B.operasi pada pengurangan

tidak ada bedanya dengan penjumlahan kita harus menyakan penyebutnya terlebih dahulu,dengan cara mencari kpk dari masing-masing penyebut yg ada,setelah itu baru kita bisa mengoperasikannya.
C.operasi pada perkalian
cara mengerjakannya dengan cara langsung mengalikan anatara pembilang dengan pembilang dan penyebut dengan penyebut
D.operasi pada pembagian
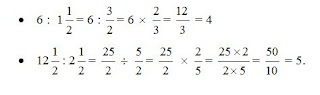
dikonsep pembagian cara mengoperasikannya dengan cara membalik antara pembilang dan penyebut di pecahan yg dibelakang tanda bagi,kemudian tanda pembagian diganti dengan tanda perkalian baru lah bisa kita operasikan kannya dengan cara dikalikan antara pembilang dengan pembilang dan penyebut dengan penyebut
A.operasi pada penjumlahan

dalam operasi ini kita harus menyamakan penyebutnya terlebih dahulu.dengan cara mencari kpk dari masing-masing penyebut tersebut,setelah itu baru kita bisa mengoperasikannya.
B.operasi pada pengurangan

tidak ada bedanya dengan penjumlahan kita harus menyakan penyebutnya terlebih dahulu,dengan cara mencari kpk dari masing-masing penyebut yg ada,setelah itu baru kita bisa mengoperasikannya.
C.operasi pada perkalian
cara mengerjakannya dengan cara langsung mengalikan anatara pembilang dengan pembilang dan penyebut dengan penyebut
D.operasi pada pembagian
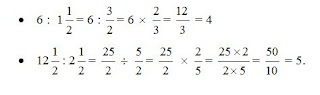
dikonsep pembagian cara mengoperasikannya dengan cara membalik antara pembilang dan penyebut di pecahan yg dibelakang tanda bagi,kemudian tanda pembagian diganti dengan tanda perkalian baru lah bisa kita operasikan kannya dengan cara dikalikan antara pembilang dengan pembilang dan penyebut dengan penyebut
Rumus
matematika mengenai bilangan
Pada materi kali ini, saya akan membahas mengenai rumus matematika yaitu tentang bilangan. Bilangan sendiri dapat diartikan sebagai
sebuah ide yang memiliki sifat abstrak dan mampu memberi keterangan mengenai
jumlah dari sebuah himpunan benda. Bilangan biasanya dinyatakan dalam bentuk
angka. Di dalam pelajaran matematika, ada banyak sekali bentuk bilangan. Mari
kita pelajari satu-persatu bilangan-bilangan tersebut.
Bilangan asli
Contohnya: {1,2,3,4,5,6,7,8,9,1,0,11,12,...}
Bilangan cacah
Contohnya: {0.1.2.3.4.5.6.7.8.9,...}
Bilangan bulat
Operasi penjumlahan dan
perkalian dalam himpunan bilangan bulat menmiliki sifat distributif yaitu:
Ax(b+c) = axb + axc
Bilangan prima
Contohnya, 3 termasuk ke dalam bilangan prima karena 3 hanya
hanya memiliki 2 buah faktor (1 dan 3) artinya 3 hanya bisa dibagi dengan 1 dan
3 dan tidak menghasilkan pecahan. Berbeda dengan angka 8, angka 8 tidak
termasuk ke dalam bilangan prima karena ia memiliki lebih dari 2 faktor yaitu
1, 2, 4, dan 8. 1 juga tidak termasuk ke dalam bilangan prima karena ia hanya
memiliki satu buah faktor yaitu angka 1 itu sendiri.
20 bilangan prima pertama adalah:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 61,
67, 71, 73, ...
Perlu kalian ketahui juga bahwa angka 2 adalah satu-satunya
bilangan prima yang bersifat genap.
Bilangan
riil
Bilangan rasional adalah
bilangan riil yang bisa kita tuliskan dalam bentuk a/b dengan a dan b adalah
bilangan bulat dimana b≠0. Contohnya adalah 42 dan 123/129.
METODE
BLAJAR MATEMATIKA
Kebanyakan orang Indonesia menganggap bahwa
matematika adalah pelajaran yang sulit. Betul kan guys?.... Karena itu, tidak
mengherankan apabila sering kali nilai matematika adalah nilai terendah yang
dijumpai oleh orang tua dalam raport anaknya. Tetapi, sesungguhnya menguasai pelajaran
matematika bukanlah hal yang teramat sulit.
Kesulitan dalam belajar
matematika bukan disebabkan oleh sulitnya materi pelajaran, melainkan karena
cara pengajaran yang tidak mudah dimengerti atau tidak sesuai dengan karakter
cara belajar si anak. Dengan menggunakan teknik belajar yang tepat, maka
pelajaran matematika akan menjadi lebih mudah dan menyenangkan untuk
dipelajari.
Dewasa ini terdapat
banyak lembaga yang mengajarkan matematika dengan cara yang unik dan menarik
yang dapat memperbaiki kemampuan anak-anak dalam belajar matematika.
Lembaga-lembaga ini memiliki teknik yang berbeda-beda untuk membuat pelajaran
matematika lebih mudah untuk dikuasai.
Berikut ini lima teknik
atau metode belajar matematika yang membuat matematika menjadi mudah untuk
dipelajari:
1. Metode Kumon
Kumon adalah metode
pengajaran yang dikembangkan pertama kali oleh seorang guru matematika asal
Jepang bernama Toru Kumon. Level awal untuk setiap anak tidak ditentukan
berdasarkan tingkatan kelas atau usia, melainkan mulai dari level yang dapat ia
kerjakan sendiri dengan mudah tanpa ada kesalahan.
Dalam kursus yang
biasanya berlangsung seminggu 2 kali ini, anak akan diberi lembar kerja yang
harus dikerjakan setiap hari di rumah. Dengan demikian, orang tua pun memegang
peranan penting untuk mengawasi cara belajar anak di rumah.
Tak perlu takut anak akan
menemukan soal-soal yang tidak dipahami dalam lembar kerja. Lembar kerjanya
sendiri telah didesain sesuai dengan level anak, sehingga ia dapat memahami
sendiri bagaimana menyelesaikan soal-soal tersebut. Selain itu, lembar kerja
juga disusun secara sistematis, cermat, dan small steps (perbedaan antar topik
bahasan tidak terlalu besar) yang dapat membantu membentuk kemampuan dasar
matematika yang baik pada anak, sehingga memungkinkan anak mengerjakan level yang
lebih tinggi tanpa kesulitan yang berarti.
2. Metode Gasing
Metode gasing (gampang,
asyik, dan menyenangkan) diciptakan oleh Prof. Yohanes Surya, yang dikenal
sebagai seorang pakar yang telah membimbing para siswa terbaik Indonesia untuk
menjuarai Olimpiade matematika dan sains di tingkat dunia.
Lewat metode ini siapapun
juga dapat belajar dan mengerti matematika. Dalam metode ini para peserta
diminta untuk memahami konsep matematika sebelum mengerjakan soal latihan yang
cukup banyak.
Topik yang dipelajari
untuk menguasai pelajaran SD (kelas 1-6) adalah:
·
Penjumlahan
·
Perkalian
·
Pengurangan
·
Pembagian
·
Bilangan negatif
·
Aplikasi 1
·
Pecahan
·
Desimal
·
Aplikasi 2
·
Geometri (termasuk keliling, luas, skala dan sistem koordinat)
·
Tiap hari siswa belajar 4 jam (lewat program ekstra kurikuler
ataupun lewat program khusus). Dalam waktu 4-6 bulan siswa akan mampu menguasai
bahan kelas 1 sampai kelas 6.
Yang membedakan
pembelajaran ini dengan pembelajaran matematika yang lain adalah:
·
Cara siswa belajar penjumlahan yang hasilnya dibawah 20.
Banyak siswa kesulitan menjumlahkan 8 + 9 = , 6 + 7 =, dsb
·
Penjumlahan dengan cara mencongak, baik penjumlahan 2 digit, 3
digit ataupun berapa digit pun
·
Cara menghafal perkalian 1 sampai 10
·
Perkalian dengan cara mencongak untuk 2 digit x 1 digit, 2 digit
x 2 digit
·
Pembagian dan pengurangan dengan cara mencongak
·
Pemanfaatan bilangan dengan negatif dalam berbagai aplikasi
penjumlahan, perkalian, pembagian dan pengurangan.
·
Pecahan dan desimal dengan cara mencongak
3. Metode Jarimatika
Jarimatika
(singkatan dari jari dan aritmatika) adalah metode berhitung dengan menggunakan
jari tangan. Metode ini dikembangkan oleh Septi Peni Wulandani
sekitar tahun 2004. Meski hanya menggunakan jari tangan, tapi dengan metode
jarimatika mampu melakukan operasi bilangan KaBaTaKu (Kali Bagi Tambah Kurang)
sampai dengan ribuan.
Jarimatika adalah
sebuah cara sederhana dan menyenangkan mengajarkan berhitung dasar kepada
anak-anak menurut kaidah : Dimulai dengan memahamkan secara benar terlebih
dahulu tentang konsep bilangan, lambang bilangan, dan operasi hitung dasar,
kemudian mengajarkan cara berhitung dengan jari-jari tangan.Prosesnya diawali,
dilakukan dan diakhiri dengan gembira.
Metode ini sangat
mudah diterima anak. Mempelajarinya pun sangat mengasyikkan, karena jarimatika
tidak membebani memori otak dan “alat”nya selalu tersedia bahkan saat ujian
karena alatnya adalah jari tangan kita sendiri. Sebuah cara sederhana dan
menyenangkan mengajarkan berhitung dasar kepada anak-anak menurut kaidah-kaidah
berikut :
• Dimulai dengan
memahami konsep bilangan, lambang bilangan dan operasi hitung dasar
• Barulah kemudian mengajarkan cara berhitung dengan jari-jari tangan.
• Prosesnya diawali, dilakukan dan diakhiri dengan gembira.
• Barulah kemudian mengajarkan cara berhitung dengan jari-jari tangan.
• Prosesnya diawali, dilakukan dan diakhiri dengan gembira.
4. Metode Sempoa (Mental
Aritmetika)
Aritmatika Mental
diajarkan dengan menggunakan alat hitung kuno yang disebut sempoa. Sempoa yang
digunakan merupakan alat bantu penghitung manual yang telah diperbarui sesuai
dengan kaidah-kaidah Aritmatik sehingga mudah dicerna dan ditransformasikan ke
dalam mental seseorang.
Program Pendidikan Mental
Aritmatika Sempoa hanya melibatkan hitungan Penambahan, ( + ), Pengurangan ( –
), Perkalian ( x ) dan Pembagian ( : ).
Cara ini dapat
mengembangkan mental/jiwa anak-anak melalui Aritmatika Mental. Anak-anak pada
awalnya menggunakan alat bantu Sempoa setelah melewati masa yang khusus
nantinya akan dapat menghitung bilangan/angka tanpa alat bantu apapun.
Tujuan Mental Aritmatika
Tujuan Mental Aritmatika
·
Merangsang potensi otak sehingga berkembang dan mencapai fungsi
yang maksimal.
·
Melatih daya imajinasi dan kreativitas.
·
Melatih daya logika dan sistematika berpikir.
·
Melatih daya konsentrasi dan daya ingat.
·
Meningkatkan kecepatan, ketepatan dan ketelitian dalam berpikir.
·
Memupuk rasa percaya diri dan sikap mental positif.
·
Membina minat pada pelajaran matematika.
5. Metode Mathemagics
MATHEMAGICCS merupakan program pembelajaran matematika,
yang dirancang dan dikembangkan oleh Ariesandi Setyono yang menitikberatkan
pada pemahaman anak akan konsep dasar matematika yang benar. Pembelajaran
Mathemagics menggunakan berbagai macam permainan sehingga menjadi suatu
pengalaman yang sangat menyenangkan bagi anak. Pembelajaran yang dilakukan
dengan hati riang gembira akan meninggalkan kesan mendalam sehingga anak akan
lebih mudah memahami pelajaran yang diberikan.
Dalam proses
pembelajarannya, Mathemagicsakan meningkatkan rasa percaya diri anak, sehingga
mereka akan mampu dan berani untuk mengerjakan soal dan mencoba untuk
menyelesaikannya.
Mathemagics
mengajarkan metode aljabar, konsep berhitung dasar seperti penambahan,
pengurangan, perkalian, pembagian, pangkat, akar, dan pecahan, dengan
memperhatikan aspek psikologis anak. Tujuannya adalah untuk membuat
pembelajaran matematika menjadi lebih mudah untuk semua anak, dengan
mengakomodasi gaya belajar mereka masing-masing. Sebuah perubahan penting, yang
pasti dialami anak yang belajar di Mathemagics, yaitu matematika menjadi lebih
mudah dan menyenangkan. Satu pengalaman belajar yang hampir tidak pernah
dirasakan anak dalam mempelajari matematika saat ini.





















